As per wikipedia, A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers. This structure was proposed by Peter Fenwick in 1994 to improve the efficiency of arithmetic coding compression algorithms.

It’s a very interesting and clever data structure that makes use of a interesting pattern, generated by a two’s complement formula, to access the array and update elements logarithmically. Imagine the following array:

index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
cumul.freq. 0 13 21 16 45 18 67 34 184 39 74 29 108 47 95 3
index 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
cumul.freq. 440 48 87 1 131 37 71 25 235 36 67 9 106 33 48 17

Suppose I want to add 50 to the item at index 17, I’ll do it by using this code:

    void update(auto &v, size_t index, int value)
    {
        while (index < v.size()) {
            v[index] += value;
            index += (index & -index);
        }
    }
    
    // caller
    update(array, 17, 50);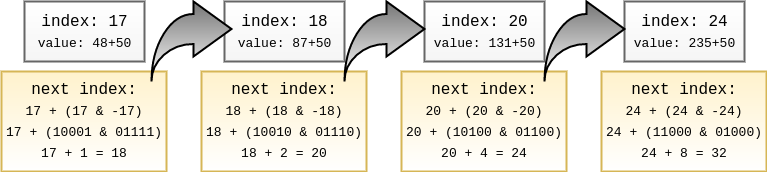

binary index tree update value

index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
cumul.freq. 0 13 21 16 45 18 67 34 184 39 74 29 108 47 95 3
index 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
cumul.freq. 440 98 137 1 181 37 71 25 285 36 67 9 106 33 48 17

Now, I’m going to read the sum of frequencies:

    int read(const auto &v, size_t index)
    {
        if (index >= v.size())
            throw exception();
    
        int s = 0;
        while (index) {
            s += v[index];
            index -= (index & -index);
        }
        return s;
    }
    
    // caller
    read(array, 31);
    $ ./bit
    896

binary index tree read value

Isolating the rightmost bit

The code index & -index is very interesting because it uses two’s complement to isolate the rightmost bit. In two’s complement, to have the negative number you need to invert all bits of the positive number and add 1.

For instance, decimal 50 is binary 110010, decimal -50 is 001101 + 1 = 001110. Performing AND operation between both will give that rightmost 1. For example, printing i & -i in a sequence of i, you will get the following pattern:

    for i in range(33):
        print i & -i,
    ...
    0 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 32

This is then used as the index (and the name) of the structure.

References